Ley de Ohm para una cadena completa y para una sección de una cadena: opciones para escribir la fórmula, descripción y explicación
No hay forma de que un electricista profesional o un especialista en electrónica pueda eludir la ley de Ohm en sus propias actividades, resolviendo cualquier problema relacionado con la instalación, ajuste y reparación de circuitos electrónicos y eléctricos.
En realidad, todo el mundo necesita entender esta ley. Porque todo el mundo tiene que lidiar con la electricidad en la vida cotidiana.
Y aunque la ley de Ohm del físico alemán está prevista en el plan de estudios de la escuela secundaria, en la práctica no siempre se estudia a tiempo. Por lo tanto, en nuestro material consideraremos un tema tan relevante para la vida y comprenderemos las opciones para escribir la fórmula.
El contenido del artículo:
Circuito eléctrico de sección única y completo.
Considerando un circuito eléctrico desde el punto de vista de la aplicación de la ley de Ohm al circuito, cabe señalar dos posibles opciones de cálculo: para una sección separada y para un circuito completo.
Cálculo de la corriente de una sección de circuito eléctrico.
Como regla general, se considera que una sección de un circuito eléctrico es la parte del circuito que excluye la fuente de campos electromagnéticos y que tiene una resistencia interna adicional.
Por tanto, la fórmula de cálculo, en este caso, parece sencilla:
Yo = U/R,
Donde, respectivamente:
- I – fuerza actual;
- Ud. - voltaje aplicado;
- R - resistencia.
La interpretación de la fórmula es simple: la corriente que fluye a través de una determinada sección del circuito es proporcional al voltaje que se le aplica y la resistencia es inversamente proporcional.
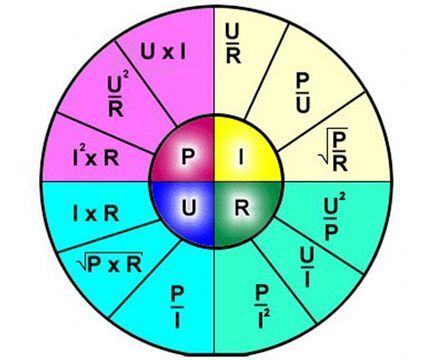
Por lo tanto, la fórmula describe claramente la dependencia del flujo de corriente a través de una sección separada del circuito eléctrico con respecto a ciertos valores de voltaje y resistencia.
Es conveniente utilizar la fórmula, por ejemplo, al calcular los parámetros de resistencia que deben soldarse en el circuito si se dan el voltaje y la corriente.
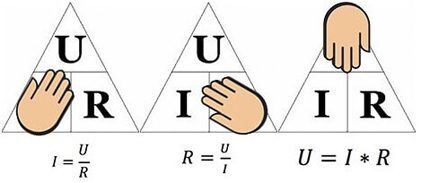
La figura anterior ayudará a determinar, por ejemplo, la corriente que fluye a través de una resistencia de 10 ohmios a la que se aplica un voltaje de 12 voltios. Sustituyendo los valores, encontramos – I = 12 / 10 = 1,2 amperios.
Los problemas de encontrar resistencia (cuando se conocen la corriente y el voltaje) o voltaje (cuando se conocen el voltaje y la corriente) se resuelven de manera similar.
Por lo tanto, siempre puede seleccionar el voltaje de funcionamiento requerido, la intensidad de corriente requerida y el elemento resistivo óptimo.
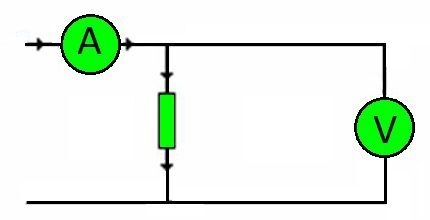
Por cierto, los cables de conexión de cualquier circuito son resistencias. La cantidad de carga que deben soportar está determinada por el voltaje.
En consecuencia, utilizando nuevamente la ley de Ohm, es posible seleccionar con precisión la sección transversal del conductor requerida, dependiendo del material del núcleo.
Tenemos instrucciones detalladas en nuestro sitio web. cálculo de la sección transversal del cable en términos de potencia y corriente.
Opción de cálculo para una cadena completa.
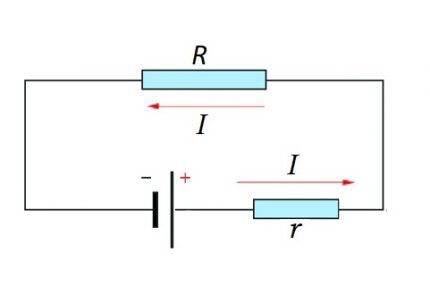
Un circuito completo se compone de una sección (secciones), así como de una fuente de EMF. Es decir, de hecho, la resistencia interna de la fuente EMF se suma al componente resistivo existente de la sección del circuito.
Por tanto, es lógico cambiar ligeramente la fórmula anterior:
Yo = U / (R + r)
Por supuesto, el valor de la resistencia interna de la FEM según la ley de Ohm para un circuito eléctrico completo puede considerarse insignificante, aunque este valor de resistencia depende en gran medida de la estructura de la fuente de la FEM.
Sin embargo, al calcular circuitos electrónicos complejos, circuitos eléctricos con muchos conductores, la presencia de resistencia adicional es un factor importante.
Tanto para una sección del circuito como para un circuito completo, se debe tener en cuenta el momento natural: el uso de corriente constante o variable.
Si los puntos mencionados anteriormente, característicos de la ley de Ohm, se consideraron desde el punto de vista del uso de corriente continua, con corriente alterna todo se ve algo diferente.
Consideración del efecto de la ley sobre una cantidad variable.
El concepto de "resistencia" a las condiciones del paso de corriente alterna debería considerarse más como el concepto de "impedancia". Esto se refiere a la combinación de una carga resistiva (Ra) y una carga de resistencia reactiva (Rr).
Tales fenómenos son causados por los parámetros de los elementos inductivos y las leyes de conmutación en relación con un valor de voltaje variable: un valor de corriente sinusoidal.
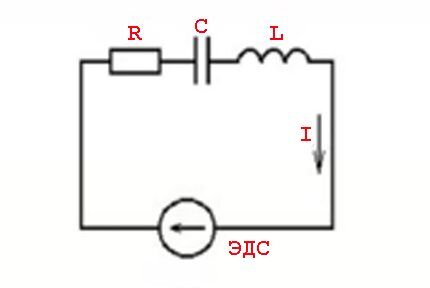
En otras palabras, existe un efecto de adelanto (atraso) de los valores de corriente con respecto a los valores de tensión, que se acompaña de la aparición de potencias activas (resistivas) y reactivas (inductivas o capacitivas).
Estos fenómenos se calculan mediante la fórmula:
Z=U/I o Z = R + J * (Xl -XC)
Dónde: z – impedancia; R – carga activa; Xl , XC – carga inductiva y capacitiva; j - coeficiente.
Conexión serie y paralelo de elementos.
Para los elementos de un circuito eléctrico (sección de un circuito), un punto característico es una conexión en serie o en paralelo.
En consecuencia, cada tipo de conexión va acompañado de un patrón diferente de flujo de corriente y suministro de voltaje.En este sentido, la ley de Ohm también se aplica de forma diferente, según la opción de inclusión de elementos.
Circuito de elementos resistivos conectados en serie.
En relación con una conexión en serie (una sección de un circuito con dos componentes), se utiliza la siguiente formulación:
- yo = yo1 = yo2 ;
- U = U1 +U2 ;
- R = R1 +R2
Esta formulación demuestra claramente que, independientemente del número de componentes resistivos conectados en serie, la corriente que fluye a través de una sección del circuito no cambia de valor.
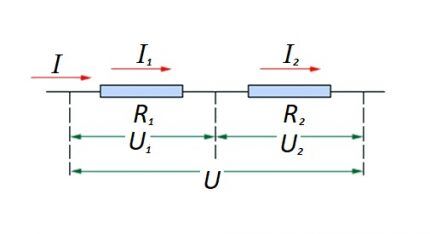
La magnitud del voltaje aplicado a los componentes resistivos efectivos del circuito es la suma y totaliza el valor de la fuente fem.
En este caso, el voltaje en cada componente individual es igual a: Ux = Yo * Rx.
La resistencia total debe considerarse la suma de los valores de todos los componentes resistivos del circuito.
Circuito de elementos resistivos conectados en paralelo.
En el caso de que exista una conexión paralela de componentes resistivos, la siguiente formulación se considera justa en relación con la ley del físico alemán Ohm:
- yo = yo1 +yo2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1/R2 + …
No se excluyen las opciones para crear secciones de circuito de tipo "mixto", cuando se utilizan conexiones en paralelo y en serie.
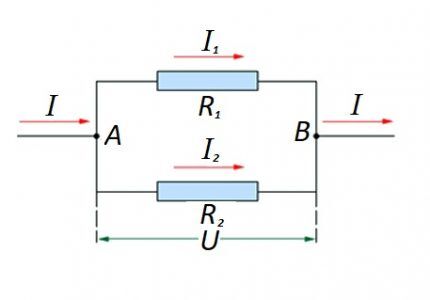
Para tales opciones, el cálculo generalmente se realiza calculando inicialmente la clasificación resistiva de la conexión en paralelo. Luego se suma al resultado obtenido el valor de la resistencia conectada en serie.
Formas integrales y diferenciales del derecho.
Todos los puntos anteriores con cálculos son aplicables a las condiciones en las que se utilizan conductores de estructura, por así decirlo, "homogénea" en circuitos eléctricos.
Mientras tanto, en la práctica, a menudo hay que lidiar con la construcción de esquemas, donde la estructura de los conductores cambia en diferentes secciones. Por ejemplo, se utilizan cables de mayor sección transversal o, por el contrario, más pequeños, fabricados de diferentes materiales.
Para tener en cuenta tales diferencias, existe una variación de la llamada "ley de Ohm diferencial-integral". Para un conductor infinitesimal, el nivel de densidad de corriente se calcula en función del valor de voltaje y conductividad.
Para el cálculo diferencial se utiliza la siguiente fórmula: J = ό * mi
Por tanto, para el cálculo integral la formulación es: Yo * R = φ1 – φ2 + έ
Sin embargo, estos ejemplos se acercan bastante a la escuela de matemáticas superiores y en realidad no se utilizan en la práctica real de un simple electricista.
Conclusiones y vídeo útil sobre el tema.
Un análisis detallado de la ley de Ohm en el siguiente vídeo ayudará a consolidar finalmente el conocimiento en esta dirección.
Una lección en video única refuerza cualitativamente la presentación teórica escrita:
El trabajo de un electricista o la actividad de un ingeniero electrónico están íntimamente relacionados con momentos en los que realmente hay que observar la ley de Georg Ohm en acción. Éstas son una especie de perogrulladas que todo profesional debería conocer.
No se requieren amplios conocimientos sobre este tema; basta con aprender las tres variaciones principales de la redacción para poder aplicarla con éxito en la práctica.
¿Le gustaría complementar el material anterior con comentarios valiosos o expresar su opinión? Por favor escriba comentarios en el bloque debajo del artículo. Si tienes alguna duda, no dudes en consultar a nuestros expertos.



